Manifolds and Tensors
Manifolds
Definition
A manifold is a topological space that locally resembles Euclidean space near each point. More formally, an n-dimensional manifold is a space where every point has a neighborhood that is homeomorphic to an open subset of Rⁿ. This means that for any point on the manifold, you can find a small region around it that behaves like n-dimensional Euclidean space.
Examples
- Circle (S¹): The circle is a 1-dimensional manifold because each point on the circle has a neighborhood that looks like an open interval in R¹.
- Sphere (S²): The sphere is a 2-dimensional manifold because each point on the sphere has a neighborhood that looks like an open disk in R².
- Torus (T²): The torus is a 2-dimensional manifold because each point on the torus has a neighborhood that looks like an open disk in R².
Charts and Atlases
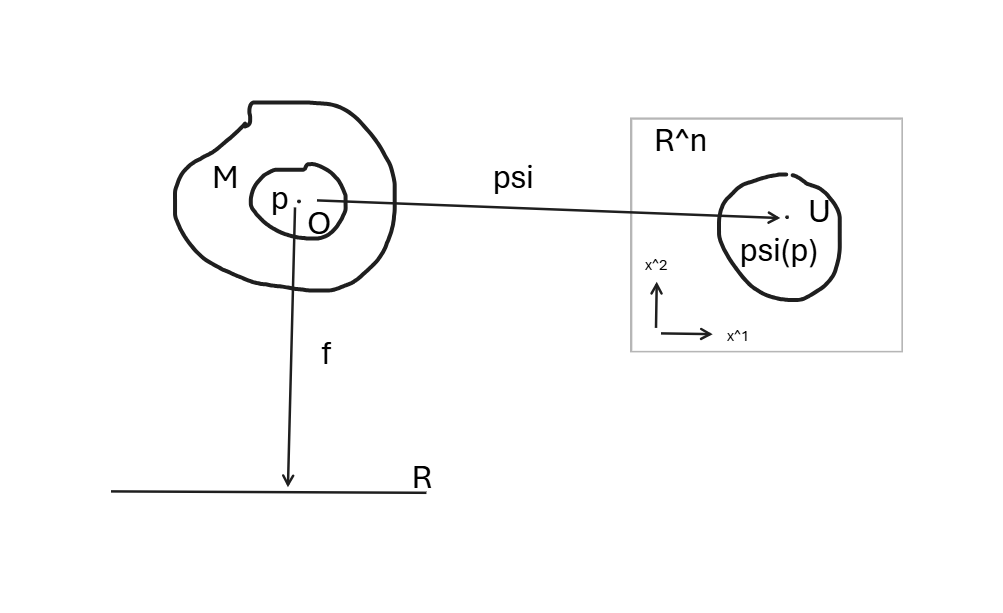
To work with manifolds, we use charts and atlases. A chart is a homeomorphism from an open subset of the manifold to an open subset of Rⁿ. An atlas is a collection of charts that cover the entire manifold. The transition maps between overlapping charts must be smooth (infinitely differentiable) for the manifold to be considered a smooth manifold.
Homeomorphism:
Two topological spaces X and Y are homeomorphic if there exists a continuous bijection f: X → Y with a continuous inverse f⁻¹: Y → X. This means that X and Y have the same topological structure, even if they may look different geometrically.
Tensors
Definition
A tensor is a mathematical object that generalizes scalars, vectors, and matrices. Tensors can be thought of as multi-dimensional arrays of numerical values that transform according to specific rules under changes of coordinates. The rank (or order) of a tensor indicates the number of indices required to specify its components.
- A scalar is a rank-0 tensor (a single number).
- A vector is a rank-1 tensor (a one-dimensional array).
- A matrix is a rank-2 tensor (a two-dimensional array).
Examples
- Scalar (Rank-0 Tensor): A single number, such as temperature or mass.
- Vector (Rank-1 Tensor): A list of numbers, such as velocity or force, represented as (v₁, v₂, v₃) in R³.
- Matrix (Rank-2 Tensor): A two-dimensional array of numbers, such as a transformation matrix in linear algebra.
- Higher-Rank Tensors: Tensors of rank 3 or higher, such as the stress tensor in continuum mechanics, which has components that depend on three indices.
Transformation Properties
Tensors transform in a specific way under changes of coordinates. For example, a rank-2 tensor T with components Tᵢⱼ transforms according to the rule: $$T’ᵢⱼ = ∑ₖₗ (∂x’ᵢ/∂xₖ)(∂x’ⱼ/∂xₗ) Tₖₗ$$ where (∂x’ᵢ/∂xₖ) are the components of the Jacobian matrix of the coordinate transformation. This ensures that the tensorial nature of T is preserved under coordinate changes.#### Applications Tensors are widely used in various fields of science and engineering, including:
- Physics: In general relativity, the Einstein field equations describe the gravitational interaction using the metric tensor.
- Engineering: In continuum mechanics, stress and strain tensors describe the internal forces and deformations in materials.
- Computer Science: In machine learning, tensors are used to represent multi-dimensional data structures in frameworks like TensorFlow and PyTorch.
Conclusion
Manifolds and tensors are fundamental concepts in mathematics and physics that provide a framework for understanding complex structures and relationships in various fields. Manifolds allow us to generalize the notion of space, while tensors provide a powerful tool for describing physical quantities and their transformations. Together, they form the backbone of many advanced theories and applications in science and engineering.
Theorem 2.2.1.
Let M be an n-dimensional manifold. Let $p \in M$ and let $V_p$ denote the tangent space at $p$. Then $dim(V_p) = n$.
Proof
Find a basis of $V_p$ by finding four linerarly independent tangent vectors which span $V_p$. Let $\psi:O\to U\subset\mathbb{R}^n$ be a chart with $p\in O$.